Emacs Calculator

你知道Emacs附带了一个计算器吗?Woop-dee-doo !电话按!哇，一个完整的计算器!

实际上，它不仅是一个简单的计算器,而是一个代数计算系统!把它名为计算器是不公平的。这太保守了，我肯定这导致了许多人忽视它。我最终是在彻底(重新)阅读Emacs手册时才遇到了它，我自己也几乎跳过了它。

几年前Will Wright在游戏 孢子 中的演示可曾见过?玩家开始是一个单细胞生物，然后进化成一个星际文明。当他开始演示时，他通过一个看起来像显微镜的东西展示了一个细胞。当时还没有人知道这个游戏是做什么的，所以每次他把范围扩大，从细菌到动物，从动物到文明，从文明到太空旅行，从行星间旅行到星系间旅行，都会引起观众的巨大反响。就像电视广告里说的:“但这还不是全部!!”

在我阅读Emacs calc手册的过程中，我不断地被它的能力所震惊，能力范围也在不断地扩大。每个新页面几乎都在说，“但这还不是全部!!”

我会像广告片一样快速过一遍它的一些功能。要查看全面的介绍请参阅calc手册。手册中有一些练习，展示了一些坑和有趣的功能交互。

按下 C-x * c 或 M-x calc 启动Calculator。会显示两个新窗口(Emacs窗口)，一个是计算器，另一个时历史记录(“跟踪”)。

首先，计算器是基于堆栈上运行的，所以它的基本用法遵循RPN。 堆栈垂直向下构建。输入数字并按回车键将其推入堆栈。操作符可以直接在数字后面输入，所以不需要一直回车。 由于负数(-)被用于减法，所以用下划线=_=表示负数。 一个包含3、4和10的堆栈示例如下所示，

3: 3
2: 4
1: 10
.

10位于堆栈的“顶部”(由“1:”表示)，因此如果我们键入一个 *, 则前两个元素相乘。像这样,

2: 3
1: 40
.

The calculator has no limitations on the size of integers, so you work with large numbers without losing precision. For example, we'll take 2^200. calculator对整数的大小没有限制，因此您可以处理大数字而不会丢失精度。例如，我们取=2^200=。

2: 2
1: 200
.

应用 ^ 运算符，

1: 1606938044258990275541962092341162602522202993782792835301376
.

但这还不是全部!!它支持复数，用括号(实、虚)输入。复数可以像其他数字一样被操作。取 -1 + 2i - 4 + 2i,

2: (-1, 2)
1: (4, 2)
.

使用 - 做减法,

1: -5
.

Then take the square root of that using Q, the square root function. 用 Q (平方根函数)然后取其平方根。

1: (0., 2.2360679775)
.

我们可以用 p 来设置精度。默认是12个位置，这里显示的时 1 / 7 的结果。

1: 0.142857142857
.

如果我们把精度调整到50，再做一次，

2: 0.142857142857
1: 0.14285714285714285714285714285714285714285714285714
.

数字也可以用各种表示法表示，比如定点表示法、科学表示法和工程表示法。不同表示法之间切换不会丢失任何信息(存储的格式与显示的格式是分开的)。

But that's not all!!! We can represent rational numbers precisely with ratios. These are entered with a :. Push on 1/7, 3/14, and 17/29, 但这还不是全部!!我们可以用比率精确地表示有理数。方法是使用 : 输入. 让我们输入 1/7, 3/14, 17/29,

3: 1:7
2: 3:13
1: 17:29
.

把它们相乘，得到最终结果，

1: 51:2842
.

有一个模式让你自动完成这些运算。

但这还不是全部!!我们可以改变基数。使用 基数# 做前缀输入一个基数不同的数字。下面是我们在base-2中输入29的方法，

2#11101

我们可以用 d r 改变显示的基数。例如堆栈上有29，按基数4展示为，

1: 4#131
.

以16为基，

1: 16#1D
.

以36为基,

1: 36#T
.

但这还不是全部!!我们可以使用撇号 ' 将代数表达式输入堆栈。符号可以作为表达式的一部分以其输入。注意:RPN中无法输入这些表达式。

1: a^3 + a^2 b / c d - a / b
.

有一个“big”模式(d B)，便于阅读，

          2
     3   a  b   a
1:  a  + ---- - -
         c d    b

    .

我们可以通过给变量赋值来计算表达式。如果我们将 a 赋值为10(10ssa)然后使用 "evaluates-to" 运算符(=),

          2
     3   a  b   a             100 b   10
1:  a  + ---- - -  =>  1000 + ----- - --
         c d    b              c d    b

    .

但这还不是全部!!它还支持向量类型可以用于处理向量,矩阵以及线性代数。它们用括号输入, [].

2:  [4, 1, 5]
1:  [ [ 1, 2, 3 ]
      [ 4, 5, 6 ]
      [ 6, 7, 8 ] ]
    .

然后取点积(*)，再取这个向量和矩阵的外积，

2:  [38, 48, 58]
1:  [ [ -14, -18, -22 ]
      [ -19, -18, -17 ]
      [ 15,  18,  21  ] ]
    .

它支持你能想到的任何矩阵和向量运算，包括map和reduce(而且可以应用与自己定义的表达式)。

我们可以用它来解线性方程组。用 a 和 b 的形式求出 x 和 y 的值，

x + a y = 6
x + b y = 10

输入(注意我们使用符号 ' 的方式输入的)，

2:  [6, 10]
1:  [ [ 1, a ]
      [ 1, b ] ]
.

然后做除法(/),

          4 a     4
1:  [6 + -----, -----]
         a - b  b - a

    .

But that's not all!!! We can create graphs if gnuplot is installed. We can give it two vectors, or an algebraic expression. This plot of sin(x) and x cos(x) was made with just a few keystrokes, 但这还不是全部!!如果安装了gnuplot，我们可以用它做图。我们可以给它两个向量，或者一个代数表达式。这张 sin(x) 和 x cos(x) 的图只需要敲几下键就生成了，

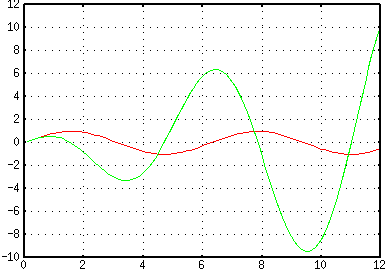
但这还不是全部!!它还提供一个HMS类型用于处理时间和角度。2小时，30分钟，4秒，等等，

3: 2@ 30' 4"
2: 4@ 22' 13"
1: 1@ 2' 56"
.

当然，一般操作符可以支持。我们可以把它们都加起来，

1: 7@ 55' 13"
.

我们可以在时间和弧度，角度等之间进行转换。

但这还不是全部!!计算器还有一个日期类型，输入在尖括号内, <> (在代数输入模式下)。它在输入日期时非常灵活。我们可以用 t N 插入当前日期。

1: <6:59:34pm Tue Jun 23, 2009>
.

如果我们让它与数字相加，数字就被当作天数。添加4,

1: <6:59:34pm Sat Jun 27, 2009>
.

它也支持刚才说的HMS格式。减去 2@ 3' 15".

1: <4:56:32pm Sat Jun 27, 2009>
.

但这还不是全部!!它还提供了一个模数形式来执行模数运算。例如，17 mod 24，

1: 17 mod 24
.

加 10，

1: 3 mod 24
.

这对 n^p mod M 这样的形式特别有用，calc可以有效地处理这种形式的运算。 例如 3^100000 mod 24. 简单的方法是先求出 3^100000,然后取模。这涉及到一个计算昂贵的中间步骤,即计算 3^100000, 这是一个巨大的数字。模块化形式则更聪明。

但这还不是全部!!计算器可以进行单位转换。我现在的Emacs版本(22.3.1)可以识别159个不同的单元。例如，我把65英里每小时推到堆栈上，

1: 65 mph
.

Convert to meters per second with u c, 输入 u c 换算成米每秒，

1: 29.0576 m / s
.

它可以灵活混合各种类型的单位。例如，我输入3立方米(' 3 m^3)，

       3
1:  3 m

    .

可以换算成加仑，

1: 792.516157074 gal
   .

我在一个没有互联网的实验室工作，所以当我需要做各种转换时，Emacs是必不可少的。

光速也是一个单位。我可以输入 1 c 然后转换成米每秒，

1: 299792458 m / s
.

但这还不是全部!!就像我说的，它是一个计算机代数系统，所以它能理解符号数学。还记得之前的代数表达式吗? 我对他们进行操作。让我们把一些表达式放到堆栈上，

3:  ln(x)

       2   a x
2:  a x  + --- + c
            b

1:  y + c

    .

前两项相乘，然后加上第三项，

                2   a x
1:  ln(x) + (a x  + --- + c) (y + c)
                     b

    .

用 a x 展开，然后用 a s 简化，

                 2   a x y              2   a c x    2
1:  ln(x) + a y x  + ----- + c y + a c x  + ----- + c
                       b                      b

    .

现在，让我们来看最酷的功能之一:微积分。使用 a d 对x求导，

    1             a y             a c
1:  - + 2 a y x + --- + 2 a c x + ---
    x              b               b

    .

或者撤销(U)后求积(a i)，

                       3      2                  3        2
                  a y x    a x  y           a c x    a c x       2
1:  x ln(x) - x + ------ + ------ + c x y + ------ + ------ + x c
                    3       2 b               3       2 b

    .

这是太棒了!一个文本编辑器能做微积分!

这就是Calc的主要特点。所有这些都让人感到繁杂，而这还只是皮毛。

自然，它还可以通过一些elisp扩展,甚至专门为此提供了一个 defmath 宏。

我打赌(希望?)有一天它会有做拉普拉斯和傅里叶变换的函数。